Theoretical calculation of a variable area flow meter
A variable area flow meter basically consists of:- A conically shaped pipe that is mounted vertically and in which the cross-section of the pipe increases towards the top.
- A float that can move freely in the pipe
The flow of the medium pushes the float upwards and gravity pulls it downwards.
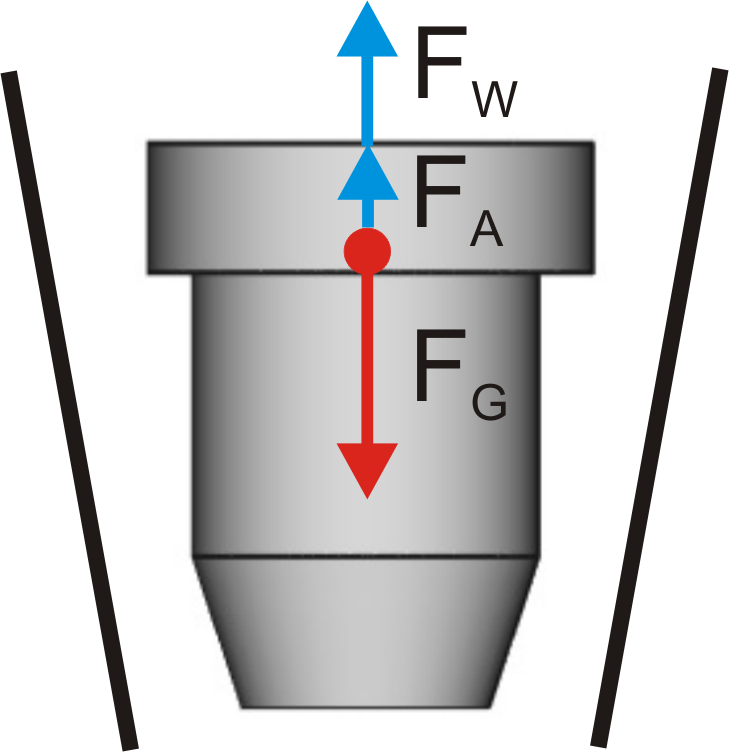
FW = FG - FA
- Flow force FW
The flow force FW, which pushes the float upwards, depends on the flow rate and the aerodynamic properties (shape) of the float. It is calculated using the formula known from aerodynamics.
FW= 0,5 ⋅ ρR ⋅ v² ⋅ CW ⋅ A
ρR: Density of the medium in the annular gap between the float and the measuring tube. [kg/m³].
This can deviate from the normal medium density (ρM) in compressible media (gases).
As ρR is difficult to calculate, the normal medium density (ρM) is often used in practice.
The difference is taken into account by the empirically determined CW-value.
v: Flow velocity of the medium in the annular gap[m/s]
CW: Drag coefficient (depending on the shape and surface properties of the float),
the surface of the measuring tube and the Reynolds number [dimensionless]
A: Cross-sectional area of the float (projection area = largest diameter) [m²]
- Weight force of the float FG
FG= ρS ⋅ VS ⋅ g
ρS: Density of the float [kg/m³]
VS: Volume of the float [m³]
g: Acceleration due to gravity 9.81 [m/s]
- Buoyancy of the float FA
A= ρM ⋅ VS ⋅ g
ρM: Density of the medium [kg/m³]
VS: Volume of the float [m³]
g: Acceleration due to gravity 9.81 [m/s]
- Relationship between flow velocity and volume flow
The flow velocity v of the variable area flow meter is directly related to the volume flow Q
Q= v⋅AR
v: Flow velocity of the medium in the annular gap [m/s]
AR: Free cross-sectional area between float and measuring tube, at the position of the float [m²].
This is the gap through which the medium can flow.
This area changes with the height of the float.
In order to determine the theoretical volume flow of a variable area flow meter in the “floating state”, i.e. a certain height in the measuring tube, the above formulas of the individual forces are used in the basic equation.
FW = FG - FA
The result is:0,5 ⋅ ρR ⋅ v² ⋅ CW ⋅ A = (ρS ⋅ VS ⋅ g) - (ρM ⋅ VS ⋅ g)
If v² is replaced by the above formula for the volume flow Q, the final formula for calculating the volume flow is obtained after conversion and simplification:

ρR: Density of the medium in the annular gap [kg/m³]
ρS: Density of the float [kg/m³]
VS: Volume of the float [m³]
g: Acceleration due to gravity 9.81 [m/s]
AR: Free cross-sectional area between float and measuring tube, at the position of the float. [m²].
CW: Drag coefficient (depending on the shape and surface properties of the float) [dimensionslos]
A: Cross-sectional area of the float (projection area = largest diameter) [m²]
In a given variable area flow meter, the density of the float, the dimensions and volume of the
float, the density of the medium and the acceleration due to gravity remain constant when the
flow rate changes.
When the flow rate changes, only the drag coefficient and the free cross-sectional area between
the float and the measuring tube change (corresponding to the lift height of the float).
As this dependency cannot be determined purely by calculation, it must be determined
empirically by calibration.
Practical calculation of a variable area flow meter
This paragraph is currently being revised.Calculation of a scale at new conditions
The scale of the variable area flowmeters is designed in the factory for a specific fluid with properties (density, viscosity) and the operating conditions (pressure, temperature) at which the the device is used.
Most manufacturers provide design software for variable area flowmeter-conversion of a scale at new conditions, which can be used to specify the optimum device for the measurement task
Example for calculation software: http://sizing.heinrichs.eu/programs/schwebekoerper/de
The most common task for the user is to adapt the existing scale to the new conditions when operating conditions change or a different fluid is used. or when using a different fluid, to adapt the existing scale to the new conditions. Changes in the material properties and operating conditions of gases or liquids have different influences.
- Gases:
Gases are compressible, i.e. they change their volume and thus density when the pressure and temperature conditions change. Because of the low gas density and low viscosity, a change in density and viscosity with different gases usually has little influence on the measurement. - Liquids:
Liquids are normally non-compressible, i.e. they do not or only slightly change their volume and thus their density with changes in pressure and temperature.
A change in pressure and temperature does not normally have to be taken into account for the same fluid. However, other viscosity or density values for different liquids have a great influence on the measurement. It may also be necessary to take into account changes in the viscosity of the liquid caused by a change in temperature.
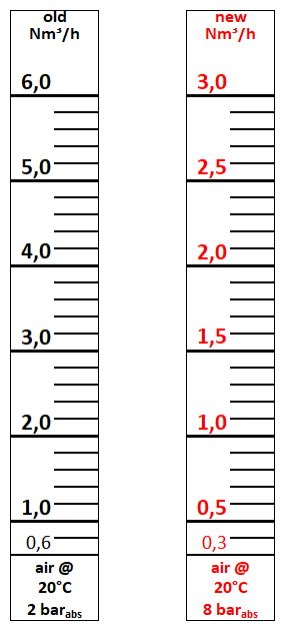
Factor calculation for gases:
- Calibrated scale in standard volume (e.g. Nm³/h)
New scale values = factor x calibrated scale values
p cal = Absolute pressure of calibrated scale, p new = Absolute pressure of new scale, T cal = Temperature of the calibrated scale in Kelvin, T new = Temperature of the new scale in Kelvin, d cal= Density of the gas of the calibrated scale, d new= Density of the gas of the new scale
Kelvin = 273 + °C - Calibrated scale in operating volume (e.g. m³/h)
New scale values = factor x calibrated scale values
pcal = Absolute pressure of calibrated scale, pnew = Absolute pressure of new scale, Tcal = Temperature of the calibrated scale in Kelvin, Tnew = Temperature of the new scale in Kelvin, dcal= Density of the gas of the calibrated scale, dnew= Density of the gas of the new scale
Kelvin = 273 + °C
Example of an Nm³/h air scale calibrated at 2 barabs.. New operating pressure 8 barabs.