Schwebekörper Durchflussmesser

Berechnung

Die Skala der Schwebekörper Durchflussmesser sind werksseitig ausgelegt für ein bestimmtes Fluid mit seinen Stoffeigenschaften (Dichte, Viskosität) und die Betriebsbedingungen (Druck, Temperatur) bei der das Gerät verwendet wird.

Die meisten Hersteller stellen dazu eine Auslegungs-Software zur Verfügung, mit denen das optimale Gerät für die Messaufgabe spezifiziert werden kann.

Beispiel Auslegungssoftware: http://sizing.heinrichs.eu/programs/schwebekoerper/de

Die häufigste Aufgabe für den Anwender besteht darin, bei veränderten Betriebsbedingungen oder bei Verwendung eines anderen Fluid, die vorhandene Skala den neuen Bedingungen anzupassen. Dabei haben Änderungen der Stoffeigenschaften und Betriebsbedingungen bei Gasen oder Flüssigkeiten unterschiedlichen Einfluss.

• Gase-Umrechnung Skala:
  Gase sind kompressibel, dh. sie verändern ihr Volumen und somit die Dichte bei Änderung der Druck- und Temperaturverhältnisse.
  Wegen der geringen Gasdichte und geringen Viskosität hat eine Änderung der Dichte und Viskosität bei unterschiedlichen Gasen meist wenig Einfluss auf die Messung.
• Flüssigkeiten-Umrechnung Skala:
  Flüssigkeiten sind normalerweis nicht-kompressibel, dh. sie verändern ihr Volumen und somit ihre Dichte bei Druck und Temperaturänderungen nicht oder nur wenig.
  Eine Änderung von Druck und Temperatur muss bei gleicher Flüssigkeit, somit normalerweise nicht berücksichtigt werden. Großen Einfluss auf die Messung haben jedoch andere Viskositäts- oder Dichtewerte bei unterschiedlichen Flüssigkeiten. Eventuell ist auch durch eine Temperaturänderung verursachte Viskositätsänderung der Flüssigkeit zu berücksichtigen.

• Faktorberechnung für Gase: Kalibrierte Skala in Normvolumen (z.B. Nm³/h)

  Neue Skalenwerte = Faktor x kalibrierte Skalenwerte
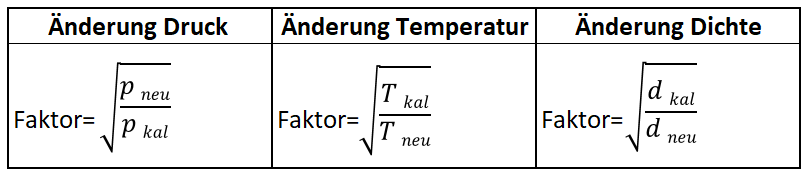
  p_kal = Absolutdruck der kalibrierten Skala, p_neu = Absolutdruck der neuen Skala, T_kal = Temperatur der kalibrierten Skala in Kelvin,
  T_neu= Temperatur der neuen Skala in Kelvin, d_kal = Dichte des Gases der kalibrierten Skala, d_neu = Dichte des neuen Gases
  Kelvin = 273 + °C

• Faktorberechnung für Gase: Kalibrierte Skala in Betriebsvolumen (z.B. m³/h)

  Neue Skalenwerte = Faktor x kalibrierte Skalenwerte
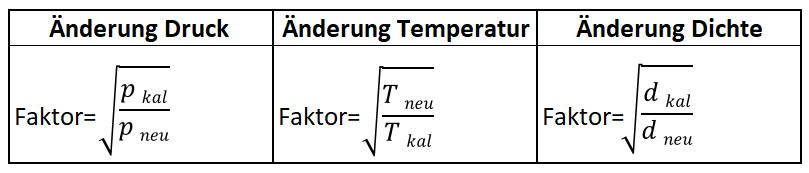
  p_kal = Absolutdruck der kalibrierten Skala, p_neu = Absolutdruck der neuen Skala, T_kal = Temperatur der kalibrierten Skala in Kelvin,
  T_neu = Temperatur der neuen Skala in Kelvin, d_kal = Dichte des Gases der kalibrierten Skala, d_neu = Dichte des neuen Gases
  Kelvin = 273 + °C

Beispiel für eine Nm³/h Luft Skala, kalibriert bei 2 bar_abs.. Neuer Betriebsdruck 8 bar_abs.

Wer mehr über die Berechnung von Schwebekörper Durchflussmessern wissen möchte, muss sich noch etwas gedulden.
Dieser Absatz wird gerade überarbeitet.

• Kontinuitätsgleichung aus der Strömungslehre
• Bernoulli Gleichung